tecnologia: 2015

viernes, 25 de septiembre de 2015

EL GOBIERNO DE OLLANTA HUMALA

EL GOBIERNO DE OLLANTA HUMALA

El presidente Ollanta Humala prometió ayer que durante el último año de su gestión seguirá fortaleciendo el desarrollo del país con inclusión social, aunque no anunció medidas concretas, como el aumento de sueldo que diferentes sectores le reclamaban.

Humala se presentó ayer por última vez como presidente ante el Congreso, donde dedicó poco más de una hora a hacer un recuento de las medidas, obras e inversiones realizadas en cuatro años de gestión y dijo que mantendrá su propuesta de "incluir para crecer" hasta el término de su mandato, el 28 de julio de 2016.

"En mi Gobierno el reto ha sido y seguirá siendo unir a un país fragmentado y avanzar en el cierre de esa brecha de desigualdad", enfatizó el mandatario, que según los últimos sondeos cuenta con un 19% de aprobación ciudadana.

Ollanta Humala aseguró que, además de sus promesas de campaña, ha asumido otros compromisos en ejecución "política, reformas trascendentes y obras estratégicas que se han ido realizando".

Señaló que ha buscado que se respeten los derechos a la educación y salud "de calidad", al trabajo y a recibir "un salario justo" y que el Estado "brinde las facilidades" para que sus compatriotas desarrollen "todas sus capacidades."

Aunque los analistas pronosticaban que Ollanta Humala anunciaría un aumento en el sueldo mínimo, exigido por los gremios sindicales, el gobernante no aludió a ese tema y tampoco ofreció mayores precisiones sobre las medidas que se tomarán en la lucha contra la inseguridad ciudadana y la corrupción.

El reto de la educación de calidad

Afirmó, sin embargo, que después de cuatro años de gestión "más de un millón trescientos mil peruanos han salido de la pobreza" y que "aún en tiempos de incertidumbre" Perú mantiene un crecimiento económico más elevado que otros países de la región.

"El mayor reto que tenemos como país es lograr tener una educación de calidad para todos los peruanos; por ello, emprender una reforma educativa integral ha sido una prioridad en mi Gobierno", acotó.

Señaló que el presupuesto en educación aumentó en más de 70% y ha superado los 22.000 millones de soles (más de 7.300 millones de dólares) y que también se han invertido más de 3.249 millones de soles (1.083 millones de dólares) para impulsar el deporte.

Tras hacer un prolongado recuento de los programas sociales que ha implementado para apoyar a niños, ancianos y estudiantes en extrema pobreza aseguró que "hoy Perú es el líder de gestión en política social en toda América Latina."

Ollanta Humala también destacó los avances en la lucha contra el tráfico ilícito de drogas y afirmó que "el narcotráfico ya no es un poder paralelo" en el Valle de los Ríos Apurímac, Ene y Mantaro (Vraem), la principal zona productora de hoja de coca en el país.

"Más temprano que tarde el Vraem será pacificado, así como ha sido pacificado ya el Alto Huallaga y levantado el estado de emergencia", acotó.

Los puntos más importantes del discurso de Humala, las reacciones de la oposición, las frases de la jornada y los retos del nacionalista para su quinto año de mandato en la foto interactiva que acompaña esta nota.

NÚMEROS COMPLEJOS

NÚMEROS COMPLEJOS.

Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraica mente cerrado que los contiene. El conjunto de los números complejos se designa con la notación $\scriptstyle \mathbb{C}$ , siendo $\scriptstyle \mathbb{R}$ el conjunto de los números reales se cumple que $\scriptstyle \mathbb{R}\sub\mathbb{C}$ ( $\scriptstyle \mathbb{R}$ está estrictamente contenido en $\scriptstyle \mathbb{C}$ ). Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, facilitación de cálculo de integrales, en aerodinámica, hidrodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

En matemáticas, estos números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. Este cuerpo contiene a los números reales y los imaginarios puros. Una propiedad importante que caracteriza a los números complejos es elteorema fundamental del álgebra pero que se demuestra aún en un curso de variable compleja , que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.

ORIGEN

El primero en usar los números complejos fue el matemático italiano Girolamo Cardano (1501–1576) quien los usó en la fórmula para resolver las ecuaciones cúbicas. El término “número complejo” fue introducido por el gran matemático alemán Carl Friedrich Gauss (1777–1855) cuyo trabajo fue de importancia básica en álgebra, teoría de los números, ecuaciones diferenciales, geometría diferencial, geometría no euclídea, análisis complejo, análisis numérico y mecánica teórica, también abrió el camino para el uso general y sistemático de los números complejos.

DEFINICIÓN

Se define cada número complejo z como un par ordenado de números reales: z = (a, b). A su vez el primer elemento a se define como parte real de z, se denota $a = Re(z)$ ; el segundo elemento b se define como parte imaginaria de z, se denota $b= Im(z)$ . Luego en el conjunto ℂ de los números complejos, se definen tres operaciones y la relación de igualdad:

Suma

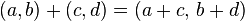
$(a, b) + (c, d) = (a+c,\, b+d)$

Producto por escalar

$r(a, b) = (ra,\, rb)$

Multiplicación

$(a, b) \cdot (c, d) = (ac - bd, ad + bc)$

Igualdad

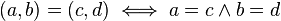
(a, b) = (c, d) \iff a = c \and b = d

REPRESENTACIONES

Representación binómica

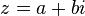$z = a + bi \,$ Un número complejo se representa en forma binomial como:

La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación:

$a = \hbox{Re}(z)=\Re(z)$

$b = \hbox{Im}(z)=\Im(z)$

Representación polar $\textstyle{\phi} = \arctan \left(\frac{b}{a}\right) = \arctan \left( \frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right) = -\arctan \left ( -\frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right)$

$\cos \phi = \frac{a}{r} \ , \ \sin \phi = \frac{b}{r}$

Despejamos a y b en las expresiones anteriores y, utilizando la representación binomial:

$z = a + \mathrm{i}b ;\; z = r\cos{\phi} + \mathrm{i}r\sin{\phi}$

Sacamos factor común r:

$z = r \left( \cos{\phi} + \mathrm{i}\sin{\phi} \right)$

Frecuentemente, esta expresión se abrevia convenientemente de la siguiente manera:

$\ z = r \; \operatorname{cis} \; {\phi}$

la cual solo contiene las abreviaturas de las razones trigonométricas coseno, la unidad imaginaria y la razón seno del argumento respectivamente.

Según esta expresión, puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.

Según la Fórmula de Euler, vemos que:

$\cos{\phi} + \mathrm{i}\sin{\phi} = e^{\mathrm{i}\phi} ;\; z = r e^{i\phi}$

No obstante, el ángulo $\phi$ no está unívocamente determinado por z, pueden existir infinitos números complejos que tienen el mismo valor representado en el plano, que se diferencian por el número de revoluciones, ya sean de sentido antihorario (positivas) u horario (negativas) las cuales se representan por números enteros $k\in\mathbb{Z}$ , como implica la fórmula de Euler:

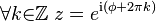
$\forall{k}{\in}\mathbb{Z}\; z= e^{\mathrm{i}(\phi + 2\pi{}k)}$

Por esto, generalmente restringimos $\phi$ al intervalo [-π, π) y a éste $\phi$ restringido lo llamamos argumento principal de z y escribimos φ=Arg(z). Con este convenio, las coordenadas estarían unívocamente determinadas por z.

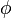En esta representación, $\textstyle{r}$ es el módulo del número complejo y el ángulo $\textstyle{\phi}$ es el argumento del número complejo.

ctor de posición (azul) en un diagrama de Argand; $a+bi$ es la expresión binomial del punto.

HISTORIA DE HUANCAVELICA

HISTORIA DE HUANCAVELICA:

La ciudad de Huancavelica fue fundada por el alcalde Mayor de Minas Francisco de Angulo el 4 de Agosto de 1571, con el nombre de Villa Rica de Oropesa, 7 años después del descubrimiento de la minas de mercurio, por la real orden del Virrey Toledo, Conde de Oropesa.

Huancavelica fue fundada con la finalidad de ejercer un mejor control de los impuestos por parte de la corona española.

En esa época del virreinato las minas de azogue de Santa Bárbara ubicada a 3,675 m.s.n.m. en los Andes centrales era la segunda más importante mina del continente americano después de las minas de Potosí en Bolivia, cambiando el destino de Huancavelica radicalmente.

Los españoles impulsaron la explotación de las grandes minas de azogue (mercurio) de Santa Bárbara, haciendo trabajar a la población indígena en condiciones inhumanas.

Su estratégica ubicación geográfica la convirtió en un lugar clave para el comercio interandino, este factor, sumado a la inmensa riqueza proveniente de las minas de mercurio, propició la formación de grandes fortunas locales durante la colonia.

Testimonio de este pasado de riqueza son las grandes casonas que engalanan las calles céntricas de la ciudad.

Pero la riqueza tuvo un paso fugaz por estas tierras. En el siglo XVII, como consecuencia del agotamiento de los yacimientos mineros, Huancavelica inició su paulatina decadencia como centro urbano.

En el siglo XIX, la ciudad fue escenario de importantes levantamientos indígenas, como el de Mateo Pumacahua (1814), líder indígena que se sublevó repetidas ocasiones contra la opresión de los españoles.

Fue reconocida como ciudad el 21 de Junio de 1825.

Hace más de 7000 años a.c, Huancavelica estuvo poblada por cazadores, y posteriormente por grupos de sedentarios dedicados a la experimentación de los primeros cultivos.

Huancavelica ha sido uno de los lugares más importantes para los pobladores andinos, pues existen numerosos sitios y complejos arqueológicos como las pampas y refugios de Mosoqcancha, Antaccocha, Pumaqoria, Astobamba Paturpampa; los petroglifos de Inka Wayqo, Qeromachay son evidencias que datan de 7,000 mil años a.c
Aproximadamente en el año 1,100 d.c., la región pasó a manos de los Huari, pueblo conquistador y altamente organizado de origen ayacuchano que dominó buena parte del territorio andino.
A la caída de los Huari, surgieron los Chancas quienes mantuvieron una fuerte resistencia frente a los ejércitos incaicos. Al ser incorporado este territorio al Tahuantinsuyo, los incas dispusieron construir dos importantes centros administrativos, Uchcus e Incahuasi.

En la época Virreinal Huancavelica era un departamento importante para los españoles sedientos de oro y riquezas hallaron las minas de mercurio de Huancavelica en el llamado Cerro Rico de Oropesa, lo cual motivó a la fundación de la ciudad de Huancavelica en el 1571.
El departamento de Huancavelica fue creado por el libertador don José de San Martín el 26 de abril de 1822. Sin embargo años más tarde se le quita esa designación, porque tenía poca población.

Foto del cerro rico de Oropesa en donde se encuentra las minas de mercurio.
Fue en el segundo gobierno del Presidente Gamarra que se le restablece la categoría de departamento a Huancavelica el 28 de abril de 1839.
Ya en el siglo XX, Huancavelica enfrentó junto a los departamentos del llamado trapecio andino (Apurímac y Ayacucho) una profunda crisis social que se agravó por las intensas sequías e inundaciones.
En la década del ochenta, la violencia terrorista también azotó el departamento, hundiéndola en la miseria y propiciando la masiva migración de sus pobladores hacia la costa.

En la actualidad gracias a la paz recuperada, este pueblo de campesinos y mineros distinguidos por su sencillez y hospitalidad trabaja por recuperar el esplendor de otros tiempos

FISICA

FÍSICA

La física (del lat. physica, y este del gr. τὰ φυσικά, neutro plural de φυσικός, "naturaleza") es la ciencia natural que estudia las propiedades, el comportamiento de la energía, la materia (como también cualquier cambio en ella que no altere la naturaleza de la misma), así como el tiempo, el espacio y las interacciones de estos cuatro conceptos entre sí.

La física es una de las más antiguas disciplinas académicas, tal vez la más antigua, ya que la astronomía es una de sus disciplinas. En los últimos dos milenios, la física fue considerada dentro de lo que ahora llamamos filosofía, química, y ciertas ramas de lamatemática y la biología, pero durante la Revolución Científica en el siglo XVII surgió para convertirse en una ciencia moderna, única por derecho propio. Sin embargo, en algunas esferas como la física matemática y la química cuántica, los límites de la física siguen siendo difíciles de distinguir.

El área se orienta al desarrollo de competencias de una cultura científica, para comprender nuestro mundo físico, viviente y lograr actuar en él tomando en cuenta su proceso cognitivo, su protagonismo en el saber y hacer científico y tecnológico, como el conocer, teorizar, sistematizar y evaluar sus actos dentro de la sociedad. De esta manera, contribuimos a la conservación y preservación de los recursos, mediante la toma de conciencia y una participación efectiva y sostenida.

La física es significativa e influyente, no sólo debido a que los avances en la comprensión a menudo se han traducido en nuevas tecnologías, sino también a que las nuevas ideas en la física resuenan con las demás ciencias, las matemáticas y la filosofía.

La física no es sólo una ciencia teórica; es también una ciencia experimental. Como toda ciencia, busca que sus conclusiones puedan ser verificables mediante experimentos y que la teoría pueda realizar predicciones de experimentos futuros basados en observaciones previas. Dada la amplitud del campo de estudio de la física, así como su desarrollo histórico con relación a otras ciencias, se la puede considerar la ciencia fundamental o central, ya que incluye dentro de su campo de estudio a la química, la biología y la electrónica, además de explicar sus fenómenos.

La física, en su intento de describir los fenómenos naturales con exactitud y veracidad, ha llegado a límites impensables: el conocimiento actual abarca la descripción departículas fundamentales microscópicas, el nacimiento de las estrellas en el universo e incluso conocer con una gran probabilidad lo que aconteció en los primeros instantes delnacimiento de nuestro universo, por citar unos pocos campos.

Esta tarea comenzó hace más de dos mil años con los primeros trabajos de filósofos griegos como Demócrito, Eratóstenes, Aristarco, Epicuro o Aristóteles, y fue continuada después por científicos como Galileo Galilei, Isaac Newton, Leonhard Euler, Joseph-Louis de Lagrange, Michael Faraday, William Rowan Hamilton, Rudolf Clausius, James Clerk Maxwell, Hendrik Antoon Lorentz, Albert Einstein, Niels Bohr, Max Planck, Werner Heisenberg, Paul Dirac, Richard Feynman y Stephen Hawking, entre muchos otros.