tecnologia: NÚMEROS COMPLEJOS

NÚMEROS COMPLEJOS.

Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraica mente cerrado que los contiene. El conjunto de los números complejos se designa con la notación $\scriptstyle \mathbb{C}$ , siendo $\scriptstyle \mathbb{R}$ el conjunto de los números reales se cumple que $\scriptstyle \mathbb{R}\sub\mathbb{C}$ ( $\scriptstyle \mathbb{R}$ está estrictamente contenido en $\scriptstyle \mathbb{C}$ ). Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, facilitación de cálculo de integrales, en aerodinámica, hidrodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

En matemáticas, estos números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. Este cuerpo contiene a los números reales y los imaginarios puros. Una propiedad importante que caracteriza a los números complejos es elteorema fundamental del álgebra pero que se demuestra aún en un curso de variable compleja , que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.

ORIGEN

El primero en usar los números complejos fue el matemático italiano Girolamo Cardano (1501–1576) quien los usó en la fórmula para resolver las ecuaciones cúbicas. El término “número complejo” fue introducido por el gran matemático alemán Carl Friedrich Gauss (1777–1855) cuyo trabajo fue de importancia básica en álgebra, teoría de los números, ecuaciones diferenciales, geometría diferencial, geometría no euclídea, análisis complejo, análisis numérico y mecánica teórica, también abrió el camino para el uso general y sistemático de los números complejos.

DEFINICIÓN

Se define cada número complejo z como un par ordenado de números reales: z = (a, b). A su vez el primer elemento a se define como parte real de z, se denota $a = Re(z)$ ; el segundo elemento b se define como parte imaginaria de z, se denota $b= Im(z)$ . Luego en el conjunto ℂ de los números complejos, se definen tres operaciones y la relación de igualdad:

Suma

$(a, b) + (c, d) = (a+c,\, b+d)$

Producto por escalar

$r(a, b) = (ra,\, rb)$

Multiplicación

$(a, b) \cdot (c, d) = (ac - bd, ad + bc)$

Igualdad

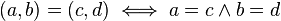
(a, b) = (c, d) \iff a = c \and b = d

REPRESENTACIONES

Representación binómica

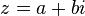$z = a + bi \,$ Un número complejo se representa en forma binomial como:

La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación:

$a = \hbox{Re}(z)=\Re(z)$

$b = \hbox{Im}(z)=\Im(z)$

Representación polar $\textstyle{\phi} = \arctan \left(\frac{b}{a}\right) = \arctan \left( \frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right) = -\arctan \left ( -\frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right)$

$\cos \phi = \frac{a}{r} \ , \ \sin \phi = \frac{b}{r}$

Despejamos a y b en las expresiones anteriores y, utilizando la representación binomial:

$z = a + \mathrm{i}b ;\; z = r\cos{\phi} + \mathrm{i}r\sin{\phi}$

Sacamos factor común r:

$z = r \left( \cos{\phi} + \mathrm{i}\sin{\phi} \right)$

Frecuentemente, esta expresión se abrevia convenientemente de la siguiente manera:

$\ z = r \; \operatorname{cis} \; {\phi}$

la cual solo contiene las abreviaturas de las razones trigonométricas coseno, la unidad imaginaria y la razón seno del argumento respectivamente.

Según esta expresión, puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.

Según la Fórmula de Euler, vemos que:

$\cos{\phi} + \mathrm{i}\sin{\phi} = e^{\mathrm{i}\phi} ;\; z = r e^{i\phi}$

No obstante, el ángulo $\phi$ no está unívocamente determinado por z, pueden existir infinitos números complejos que tienen el mismo valor representado en el plano, que se diferencian por el número de revoluciones, ya sean de sentido antihorario (positivas) u horario (negativas) las cuales se representan por números enteros $k\in\mathbb{Z}$ , como implica la fórmula de Euler:

$\forall{k}{\in}\mathbb{Z}\; z= e^{\mathrm{i}(\phi + 2\pi{}k)}$

Por esto, generalmente restringimos $\phi$ al intervalo [-π, π) y a éste $\phi$ restringido lo llamamos argumento principal de z y escribimos φ=Arg(z). Con este convenio, las coordenadas estarían unívocamente determinadas por z.

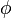En esta representación, $\textstyle{r}$ es el módulo del número complejo y el ángulo $\textstyle{\phi}$ es el argumento del número complejo.

ctor de posición (azul) en un diagrama de Argand; 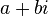$a+bi$ es la expresión binomial del punto.

tecnologia

viernes, 25 de septiembre de 2015

NÚMEROS COMPLEJOS

Representación binómica

Representación polar $\textstyle{\phi} = \arctan \left(\frac{b}{a}\right) = \arctan \left( \frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right) = -\arctan \left ( -\frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right)$

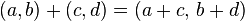
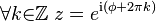
No hay comentarios.:

Publicar un comentario